§ 1.2. Интегральные и дифференциальные соотношения между основными величинами, характеризующими поле.Электромагнитные поля могут быть описаны интегральными или дифференциальными соотношениями. Интегральные соотношения относятся к объему (длине, площади) участка поля конечных размеров, а дифференциальные - к участку поля физически бесконечно малых размеров. Они выражаются операциями градиента, дивергенции, ротора (раскрытие операции grad, div и rot в различных системах координат см. в III части курса). В макроскопической теории поля описывают свойства поля, усредненные по бесконечно малому физическому объему и во времени. Этот объем в отличие от математически бесконечно малого объема может содержать большое число атомов вещества. Дифференциальные уравнения макроскопической теории поля не описывают поля внутри атомов, для чего, как известно, служат уравнения квантовой теории поля.
В электростатическом поле поток вектора напряженности электрического поля 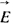 через замкнутую поверхность (рис. 1.1) равен свободному заряду через замкнутую поверхность (рис. 1.1) равен свободному заряду 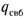 , находящемуся внутри этой поверхности, деленному на , находящемуся внутри этой поверхности, деленному на 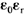 (теорема Гаусса): (теорема Гаусса):
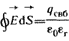 (1.1) (1.1)
где 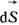 - элемент поверхности, направленный в сторону внешней нормали к объему; - элемент поверхности, направленный в сторону внешней нормали к объему; 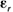 - относительная диэлектрическая проницаемость диэлектрика. - относительная диэлектрическая проницаемость диэлектрика.
В дифференциальной форме теорема Гаусса записывается так:
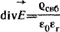 (1.2) (1.2)
(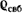 - объемная плотность свободного заряда, Кл/м3). - объемная плотность свободного заряда, Кл/м3).
Переход от (1.1) к (1.2) осуществляют делением обеих частей (1.1) на объем V, находящийся внутри поверхности S, и стремлении объема V к нулю.
Физически 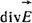 означает исток вектора в данной точке. означает исток вектора в данной точке.
В электростатическом поле и в стационарном электрическом поле на заряд q действует сила 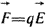 . Отсюда следует, что . Отсюда следует, что 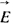 может быть определена как силовая характеристика поля может быть определена как силовая характеристика поля 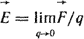 . Если q под действием сил поля переместится из точки 1 в точку 2 (рис. 1.2), то силы поля совершат работу . Если q под действием сил поля переместится из точки 1 в точку 2 (рис. 1.2), то силы поля совершат работу 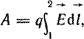 , где , где 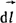 - элемент пути из 1 в 2. - элемент пути из 1 в 2.
Под разностью потенциалов U12 между точками 1 и 2 понимают работу, совершаемую силами поля при переносе заряда q = 1 Кл из точки 1 в точку 2,
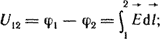 (1.3) (1.3)
U12 не зависит от того, по какому пути происходило перемещение из точки 1 в точку 2. Выражению (1.3) соответствует дифференциальное соотношение
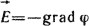 (1.4) (1.4)
Градиент φ (grad φ) в некоторой точке поля определяет скорость изменения φ в этой точке, взятую в направлении наибольшего его возрастания. Знак минус означает, что 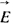 и grad φ направлены противоположно. и grad φ направлены противоположно.
Электрическое поле называют потенциальным, если для него 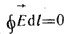 . Электрическое поле поляризованного диэлектрика описывается вектором электрического смещения (индукции) . Электрическое поле поляризованного диэлектрика описывается вектором электрического смещения (индукции)
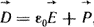 (1.5) (1.5)
где 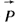 - поляризованность диэлектрика, которая равна электрическому моменту единицы объема поляризованного диэлектрика. - поляризованность диэлектрика, которая равна электрическому моменту единицы объема поляризованного диэлектрика.
В стационарном неизменном во времени электрическом поле в проводящей среде в смежные моменты времени распределение зарядов одинаково, поэтому для этого поля справедливо определение разности потенциалов по формуле 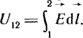 . .
Внутри источника постоянной ЭДС результирующая напряженность электрического поля 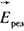 равна векторной сумме потенциальной (кулоновой) составляющей равна векторной сумме потенциальной (кулоновой) составляющей 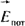 и сторонней составляющей и сторонней составляющей 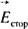 : :
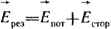
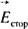 разделяет заряды внутри источника, она обусловлена химическими, электрохимическими, тепловыми и другими процессами не электростатического происхождения и направлена встречно разделяет заряды внутри источника, она обусловлена химическими, электрохимическими, тепловыми и другими процессами не электростатического происхождения и направлена встречно 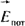 . В электромагнитном поле могут протекать электрические токи. Под электрическим током понимают направленное (упорядоченное) движение электрических зарядов. Ток в некоторой точке поля характеризуется своей плотностью . В электромагнитном поле могут протекать электрические токи. Под электрическим током понимают направленное (упорядоченное) движение электрических зарядов. Ток в некоторой точке поля характеризуется своей плотностью 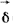 (А/м2). Известны три вида тока: ток проводимости (плотность его (А/м2). Известны три вида тока: ток проводимости (плотность его 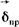 ), ток смещения (плотностью ), ток смещения (плотностью 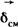 ) и ток переноса (плотностью ) и ток переноса (плотностью 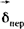 ). Ток проводимости протекает в проводящих телах под действием электрического поля, плотность его пропорциональна ). Ток проводимости протекает в проводящих телах под действием электрического поля, плотность его пропорциональна 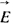
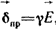 (1.6) (1.6)
где γ - удельная проводимость проводящего тела, Ом-1·м-1. В металлах ток проводимости обусловлен упорядоченным движением свободных электронов, в жидкостях - движением ионов. Плотность тока смещения в диэлектрике равна производной по времени от вектора электрического смещения 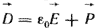 : :
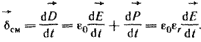
(1.7)
Слагаемое 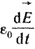 представляет собой составляющую тока смещения, обусловленную изменением во времени напряженности поля представляет собой составляющую тока смещения, обусловленную изменением во времени напряженности поля 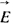 в вакууме. Носителями тока смещения в физическом вакууме (в нем нет частиц вещества) являются виртуальные частицы. Они всегда возникают парами, какбы из ничего, например, электрон и позитрон, или протон и антипротон и т. п. Каждая пара виртуальных частиц является коротко живущей (время жизни в вакууме. Носителями тока смещения в физическом вакууме (в нем нет частиц вещества) являются виртуальные частицы. Они всегда возникают парами, какбы из ничего, например, электрон и позитрон, или протон и антипротон и т. п. Каждая пара виртуальных частиц является коротко живущей (время жизни 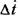 ). Составляющие ее частицы могут перемещаться на очень малое расстояние ). Составляющие ее частицы могут перемещаться на очень малое расстояние 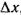 , а затем эти частицы с противоположного знака зарядами аннигилируют. Каждая виртуальная частица обладает разбросом энергии , а затем эти частицы с противоположного знака зарядами аннигилируют. Каждая виртуальная частица обладает разбросом энергии 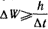 и разбросом импульса и разбросом импульса 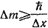 , где постоянная Планка h = 6,626 · 10-34 Дж·с. Для каждой пары виртуальных частиц выполняется закон сохранения заряда, но в рамках соотношения неопределенностей наблюдаются местные нарушения закона сохранения энергии и закона сохранения импульса. Слагаемое , где постоянная Планка h = 6,626 · 10-34 Дж·с. Для каждой пары виртуальных частиц выполняется закон сохранения заряда, но в рамках соотношения неопределенностей наблюдаются местные нарушения закона сохранения энергии и закона сохранения импульса. Слагаемое 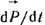 обусловлено изменением поляризованности во времени (изменением расположения связанных зарядов в диэлектрике при изменении обусловлено изменением поляризованности во времени (изменением расположения связанных зарядов в диэлектрике при изменении 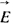 во времени). В качестве примера тока смещения может быть назван ток через конденсатор. Ток переноса обусловлен движением электрических зарядов в свободном пространстве. Примером тока переноса может служить ток в электронной лампе. Если положительный заряд объемной плотности во времени). В качестве примера тока смещения может быть назван ток через конденсатор. Ток переноса обусловлен движением электрических зарядов в свободном пространстве. Примером тока переноса может служить ток в электронной лампе. Если положительный заряд объемной плотности 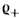 движется со скоростью движется со скоростью 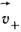 и отрицательный заряд объемной плотности и отрицательный заряд объемной плотности 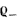 со скоростью со скоростью 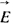 , то плотность тока переноса в этом поле , то плотность тока переноса в этом поле 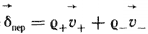 в явном виде не зависит от напряженности в явном виде не зависит от напряженности 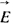 в данной точке поля. Если в некоторой точке поля одновременно существовали бы все три вида тока, то полная плотность тока в данной точке поля. Если в некоторой точке поля одновременно существовали бы все три вида тока, то полная плотность тока 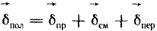 . Для большинства задач ток переноса отсутствует. . Для большинства задач ток переноса отсутствует.
Ток - это скаляр алгебраического характера. Полный ток через поверхность S равен
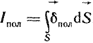 (1.8) (1.8)
Если в электромагнитном поле выделить некоторый объем, то ток, вошедший в объем, будет равняться току, вышедшему из объема, т. е.
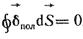 (1.9) (1.9)
где 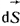 - элемент поверхности объема, он направлен в сторону внешней поотношению к объему нормали к поверхности. Последнее уравнение выражает принцип непрерывности полного тока: линии полного тока представляют замкнутые линии, не имеющие ни начала, ни конца. - элемент поверхности объема, он направлен в сторону внешней поотношению к объему нормали к поверхности. Последнее уравнение выражает принцип непрерывности полного тока: линии полного тока представляют замкнутые линии, не имеющие ни начала, ни конца.
Электрические токи неразрывносвязаны с магнитным полем. Эта связь определяется интегральной формой закона полного тока
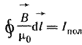 (1.10) (1.10)
циркуляция вектора по замкнутому контуру равна полному току, охваченному этим контуром; 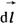 - элемент длины контура (рис. 1.3). Таким образом, все виды токов, хотя и имеют различную физическую природу, обладают свойством создавать магнитное поле. - элемент длины контура (рис. 1.3). Таким образом, все виды токов, хотя и имеют различную физическую природу, обладают свойством создавать магнитное поле.
Ферромагнитные вещества обладают спонтанной намагниченностью. Характеристикой ее является магнитный момент единицы объема вещества 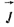 (его называют намагниченностью). Для ферромагнитных веществ (его называют намагниченностью). Для ферромагнитных веществ
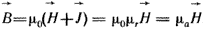 (1.11) (1.11)
где 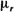 - относительная магнитная проницаемость; - относительная магнитная проницаемость; 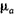 - абсолютная магнитная проницаемость. - абсолютная магнитная проницаемость.
Напряженность магнитного поля
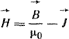 (1.12) (1.12)
равна разности двух векторных величин 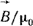 и и 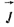 . .
Закон полного тока в интегральной форме часто записывают в виде
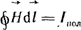 (1.13) (1.13)
или в дифференциальной форме
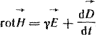 (1.14) (1.14)
Запись (1.14) закона полного тока получили из (1.13), поделив обе части его на площадь 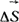 , охваченную контуром интегрирования, и стремлении , охваченную контуром интегрирования, и стремлении 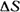 к нулю. Физический ротор (rot) характеризует поле в данной точке в отношении способности к образованию вихрей. к нулю. Физический ротор (rot) характеризует поле в данной точке в отношении способности к образованию вихрей.
Плотность тока переноса в правой части последнего уравнения не учтена, так как он обычно отсутствует в задачах, решаемых с помощью этого уравнения. Магнитный поток через некоторую поверхность S (рис. 1.4) определяют как поток вектора 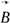 через эту поверхность через эту поверхность
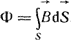 (1.15) (1.15)
Поток Φ - это скаляр алгебраического характера, измеряется в веберах (Вб). Если поверхность S замкнутая и охватывает объем V, то поток, вошедший в объем, равен потоку, вышедшему из него, т. е.
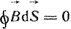 (1.16) (1.16)
Это уравнение выражает принцип непрерывности магнитного потока. Линии магнитной индукции - это замкнутые линии. В дифференциальной форме принцип непрерывности магнитного потока записывается так:
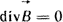 (1.17) (1.17)
В 1831 г. М. Фарадей сформулировал закон электромагнитной индукции: ЭДС eинд наведенная в некотором одновитковом контуре пронизывающим этот контур, изменяющимся во времени магнитным потоком, определяется выражением
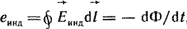 (1.18) (1.18)
здесь 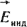 - индукционная составляющая напряженности электрического поля. Знак минус обусловлен правой системой отсчета: принято, что положительное направление отсчета для ЭДС и направление потока при его возрастании связаны правилом правого винта (рис. 1.5). - индукционная составляющая напряженности электрического поля. Знак минус обусловлен правой системой отсчета: принято, что положительное направление отсчета для ЭДС и направление потока при его возрастании связаны правилом правого винта (рис. 1.5).
Если контур многовитковый (катушка с числом витков ω), то
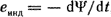 (1.19) (1.19)
здесь Ψ - потокосцепление катушки, равное сумме потоков, пронизывающих отдельные витки катушки,
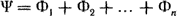 (1.20) (1.20)
Если все витки ω пронизываются одинаковыми потоками Φ, то
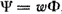
где Ψ - результирующее потокосцепление, оно может создаваться не только внешним по отношению к данному контуру потоком, но и собственным потоком, пронизывающим контур, при протекании по нему тока. В проводнике длиной 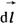 , пересекающем магнитные силовые линии неизменного во времени магнитного поля индукции , пересекающем магнитные силовые линии неизменного во времени магнитного поля индукции 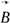 (рис. 1.6), вследствие силы Лоренца наводится ЭДС (рис. 1.6), вследствие силы Лоренца наводится ЭДС
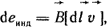 (1.21) (1.21)
где 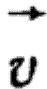 - скорость перемещения проводника относительно магнитного поля. - скорость перемещения проводника относительно магнитного поля.
В (1.21) 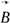 скалярно умножается на векторное произведение скалярно умножается на векторное произведение 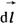 и и 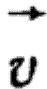 . .
Если в результате расчета по (1.21) 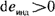 , то , то 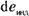 направлена по направлена по 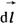 . .
В 1833 г. русский академик Э. X. Ленц установил закон электромагнитной инерции. При всяком изменении магнитного потока, сцепляющимся с каким-либо проводящим контуром, в нем возникает индуктированная ЭДС, стремящаяся вызвать в контуре ток, который: 1) препятствует изменению потокосцепления контура; 2) вызывает механическую силу, препятствующую изменению линейных размеров контура или его повороту.
Закон электромагнитной индукции, примененный к контуру бесконечно малых размеров, записывается так:
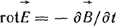 (1.22) (1.22)
(в последней формуле индукционную составляющую напряженности поля 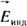 принято обозначать принято обозначать 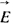 ). Обобщая, можно сказать, что электромагнитное поле описывается четырьмя основными уравнениями в интегральной форме: ). Обобщая, можно сказать, что электромагнитное поле описывается четырьмя основными уравнениями в интегральной форме:
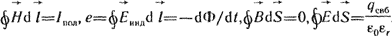 (1.23) (1.23)
Этим уравнениям отвечают четыре уравнения в дифференциальной форме:
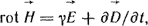 (а) (а)
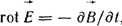 (б) (б)
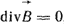 (в) (в)
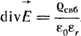 (г) (г)
Они сформулированы в 1873 г. Д. Максвеллом. Их называют уравнениями Максвелла или уравнениями макроскопической электродинамики.
Уравнение (а) означает, что вихревое магнитное поле создается токами проводимости и токами смещения. Уравнение (б) свидетельствует о том, что изменение магнитного поля во времени вызывает вихревое электрическое поле. Уравнение (в) - магнитное поле не имеет источников и уравнение (г) - что истоком линий 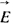 являются свободные заряды. Частные производные в уравнениях (а) и (б) учитывают, что уравнения записаны для неподвижных тел и сред в выбранной системе координат. являются свободные заряды. Частные производные в уравнениях (а) и (б) учитывают, что уравнения записаны для неподвижных тел и сред в выбранной системе координат.
|
