|
Приложение С
(справочное)
Технические обоснования метода группирования
При обосновании методов измерений, установленных в настоящем стандарте, необходимо принимать во внимание противоречивые требования к процессу измерения (например, к ширине полосы частот измерений и разрешению по частоте). Поэтому при определении на практике результатов измерений достижение компромисса при выполнении противоречивых требований является в некоторых случаях более важным, чем обеспечение наивысшей точности оценки сигнала. В настоящем приложении рассмотрены обоснования, учтенные при разрешении нескольких наиболее важных вопросов.
Примечание - В настоящем стандарте напряжение и сила тока выражены в среднеквадратичных значениях, если не указано иное.
С.1 Энергетическая эквивалентность представления сигнала во временной и частотной областях
Энергетическая теорема Релея устанавливает следующую эквивалентность мощности (или энергии) сигнала, представленного во временной и частотной областях:
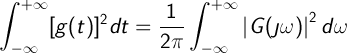 (C.1) (C.1)
где g(t) — функция времени
G(jω) — комплексное преобразование Фурье функции g(t);
ω = 2πƒ
Примечание - Так как мощность сигнала пропорциональна квадрату напряжения или тока, то выражение [g(t)]2 рассматривается как "мощность" сигнала. Поэтому, если g(t) — зависимость напряжения от времени, то левая часть выражения (В.1) (сигнал во временной области) имеет размерность В2 с ("энергии"). Преобразование Фурье сигнала g(t) представляет собой спектральную плотность напряжения и, например, G(jω) будет иметь размерность В/Гц или В•с, т.е. правая часть выражения (В.1) будет иметь размерность В2с ("энергии").
Если функция времени не является периодической, ее спектральная плотность должна быть непрерывной. Если функция является периодической, то она может быть представлена в интервале измерения длительностью TN , так как бесконечное повторение интервалов измерения будет полностью представлять функцию g(t) . Преобразование Фурье данного ограниченного во времени сигнала не является непрерывным и содержит спектральные линии, частоты которых отделены друг от друга интервалами ƒN=1/TN . Произведение длительности временного интервала измерения на квадрат среднеквадратического значения (комплексной) спектральной составляющей G2k на частоте ƒ= k׃N представляет собой (приблизительно) энергию, соответствующую непрерывной спектральной плотности в интервале частот от ƒ-ƒN /2 до ƒ+ƒN /2 . "Энергия" всех спектральных линий эквивалентна "энергии" функции времени в пределах интервала измерения. Разделив "энергию" на длительность интервала измерения, получим следующее выражение:
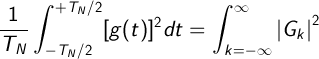 (C.2) (C.2)
Левая часть выражения (С.2) представляет собой среднюю мощность функции времени в пределах интервала измерения, правая часть выражения (С.2) - полную мощность всех спектральных линий.
Спектральные линии преобразования Фурье на отрицательных частотах являются сопряженными относительно спектральных линий при тех же положительных частотах, т.е. спектр "мощности" симметричен относительно частоты ƒ=0 . При сложении частей спектра на отрицательных и положительных частотах выражение (В.2) может быть упрощено:
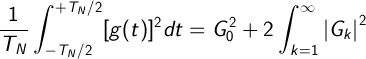 (C.3) (C.3)
Определение амплитуды ck составляющей ряда Фурье в соответствии с выражением (3) (см. раздел 3) относится к TN/2 , а не к TN (исключая c0 , который относится к TN ). Поэтому ck=2×Gk или Ck=√2Gk Выражение (С.3) может быть, следовательно, представлено в виде
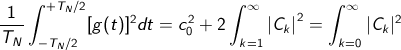 (C.4) (C.4)
Практически номера коэффициентов в сумме выражения (В.4) должны быть ограничены, т.е. K=1…K .
Если полоса частот сигнала ограничена частотой ƒ=KƒN , то "мощность" составляющих с порядковыми номерами k > K равна нулю, и они могут быть исключены из суммы в выражении (С.4). При этом необходимо, чтобы частота ƒk была вне полосы рабочих частот средства измерений.
С.2 Характеристики цифровых средств измерений
В настоящем стандарте рассмотрены цифровые СИ. В соответствии с формулой Шеннона функция времени должна быть дискретизирована с частотой отсчетов ƒs > 2ƒk , так что коэффициенты спектральных составляющих должны быть рассчитаны вплоть до Ck . Число отсчетов в измерительном окне составляет M = ƒsTN .
При идеальных условиях, указанных выше, т.е. если сигнал, преобразованный в последовательность дискретных величин, является периодическим, его полоса частот ограничена и интервал измерения синхронизирован с периодическим сигналом, выражение (С.4) может быть переписано в виде
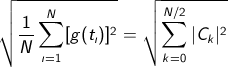 (C.5) (C.5)
где g(ti) — значения функции времени в точках взятия выборок;
ti=i×TN /N
Из выражения (С.5) следует, что среднеквадратическое значение спектральных составляющих при представлении сигнала в частотной области равно среднеквадратическому значению сигнала во временной области при его представлении в виде последовательности выборок. Поэтому энергетическая теорема Релея может быть применена для подтверждения того, что при конкретных условиях спектр мощности достаточно точно представляет сигнал во временной области.
При идеальных условиях, указанных выше, спектр мощности, рассчитанный методами, установленными в настоящем стандарте, представляет собой среднюю мощность спектральных составляющих измеряемого сигнала на установленном временном интервале измерений. Спектр мощности точно определяет полную мощность сигнала, а также мощности индивидуальных частотных составляющих и частоты этих составляющих. Для практических целей условия могут быть отнесены к "идеальным", если все составляющие измеряемого сигнала являются в точности "базовыми" гармониками, т.е. ƒN=1/TN . Учитывая жесткие требования к синхронизации, установленные в настоящем стандарте, данные условия, близкие к идеальным, по определению будут иметь место для составляющей основной частоты системы электроснабжения и для любых составляющих на частотах, кратных основной частоте, т.е. для гармоник основной частоты.
Примечание - Значение "базовой" частоты должно быть обратно длительности интервала измерения; значение основной частоты обратно длительности периода в системе электроснабжения.
Длительность временного интервала измерения (ширина измерительного окна) для СИ, соответствующих требованиям настоящего стандарта, TN ≈ 200 мс, равна 10 периодам основной частоты для систем электроснабжения 50 Гц и 12 периодам основной частоты для систем 60 Гц. СИ, сконструированные в соответствии с требованиями первого издания МЭК 61000-4-7 [8], имеют измерительное окно шириной 16 периодов основной частоты (длительность 320 мс для систем электроснабжения 50 Гц и ≈ 267 мс для систем электроснабжения 60 Гц). Частотный разнос спектральных составляющих ("базовая" частота ƒN ) для СИ, соответствующих требованиям настоящего стандарта, равен 5 Гц. Для СИ, соответствующих требованиям первого издания МЭК 61000-4-7 [8], частотный разнос спектральных составляющих 3,125 Гц - для систем электроснабжения частотой 50 Гц и 3,75 Гц - для систем электроснабжения 60 Гц.
Метод группирования, установленный в настоящем стандарте [выражение (8)], обеспечивает точную оценку полной мощности спектральных составляющих. При использовании метода группирования учитывают все спектральные составляющие, а не только спектральные линии на частотах, кратных основной частоте ("гармоники"). Выражение (8) относится только к спектральным линиям при частотном разносе 5 Гц и должно, следовательно, быть модифицировано при использовании других "базовых" частот. При правильном применении выражения (8) с учетом его модификации (при необходимости) спектр мощности точно представляет среднюю мощность измеряемого сигнала, как установлено энергетической теоремой Релея.
Для условий, которые не могут быть отнесены к идеальным, например, при наличии негармонического сигнала с составляющими на частотах ƒ ≠ k ƒN ( k — целое число), происходит определенная потеря информации о частотном содержании сигнала, но мощность сигнала будет представлена точно. При интервале измерения длительностью 200 мс наличие интергармонических составляющих на частотах, не кратных частоте 5 Гц, например, на частоте 287 Гц, будет означать наличие негармонического сигнала или присутствие колебаний напряжения в пределах анализируемого интервала измерений. Метод группирования, установленный в настоящем стандарте, обеспечивает точную оценку мощности в большинстве случаев. Распределение мощности в пределах групп, соответствующих конкретным сигналам, зависит от характеристик наложенных сигналов.
В разделах С.3-С.4 приведены несколько примеров, иллюстрирующих данный подход. Влияние колебаний гармоник напряжения и тока рассмотрено в С.3. Влияние интергармоник рассмотрено в С.4. В приведенных примерах основные составляющие напряжения и тока, являющиеся на практике преобладающими, не рассматриваются. Это позволяет детально представить на рисунках С.1-С.7 спектральные линии и эффекты группирования.
С.3 Колебания гармоник
Пример 1 - Ток пятой гармоники во временной и спектральной областях, среднеквадратическое значение которого изменяется в течение длительности интервала измерения от 3,536 до 0,707 А, представлен на рисунке С.1. Ток изменяется после 21, 25 периодов пятой гармоники. Расчетное среднеквадратическое значение тока для данного случая равно 2,367 А. Измеренное значение пятой гармоники (одиночная спектральная линия) равно 1,909 А, что без рассмотрения других спектральных линий приводит к ошибке 19,3%. Расчет значения гармонической подгруппы приводит в этом случае к значению тока 2,276 А (ошибка снижается до 3,84%). Однако расчет значения гармонической группы измеренной линии приводит уже к значению 2,332 А, что соответствует небольшой остаточной ошибке 1,47%.
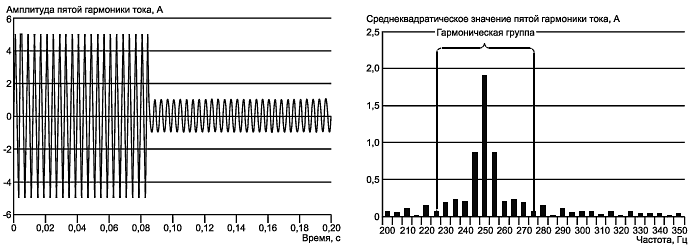
Рисунок С.1 - Колебания тока пятой гармоники
Пример 2 - Напряжения гармоник в системах электроснабжения обычно вызваны гармоническими составляющими тока, потребляемого несколькими нелинейными нагрузками. Как правило, существенная корреляция между изменениями нагрузок отсутствует. Кроме того, к системам электроснабжения подключены также квазистационарные нагрузки. Поэтому быстрые флюктуации гармоник напряжения со значительными размахами являются редкими в системах электроснабжения. Напряжение пятой гармоники во временной и спектральной областях, среднеквадратическое значение которого изменяется в течение длительности интервала измерения от 13,225 до 9, 776 В, представлено на рисунке С.2. В данном случае расчетное среднеквадратическое значение напряжения равно 11,37 В, а измеренное (одиночная спектральная линия) - 11,24 В. Установленный в настоящем стандарте алгоритм группирования приводит к значению 11,33 В для гармонической подгруппы и 11,34 В для гармонической группы (ошибки 0,35% и 0,24% соответственно). Такие ошибки находятся в пределах погрешности, установленной для средств измерений.
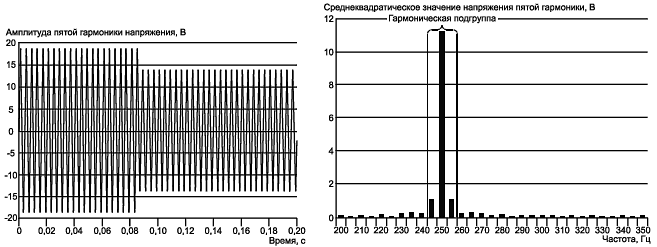
Рисунок С.2 - Колебания напряжения пятой гармоники
Пример 3 - Микроволновые печи в составе гармоник потребляемого тока создают также третью гармонику. В качестве примера рассмотрена микроволновая печь с фазовым управлением средней мощностью при частоте повторения 5 Гц и рабочем цикле 50%. Ток третьей гармоники и соответствующий спектр представлены на рисунке С.3. Значение тока третьей гармоники равно 1 А. Полное среднеквадратическое значение тока равно 0,707 А. Среднеквадратическое значение спектральной линии этой гармоники равно 0,5 А (ошибка - 29,3%). Значение гармонической подгруппы равно 0,673 А (ошибка - 4,8%), значение гармонической группы равно 0,692 А (ошибка - 2%).
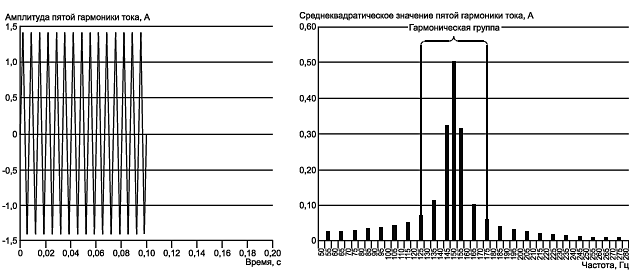
Рисунок С.3 - Колебания тока третьей гармоники микроволновой печи
С.4 Интергармоники
Пример 1 - К системам электроснабжения могут быть подключены устройства передачи/приема сигналов. С тем, чтобы исключить нарушения работы при воздействии гармоник сетевого напряжения, указанные устройства используют частоты, как правило, расположенные между частотами двух гармоник, т.е. интергармонические частоты. Если частота кратна "базовой" частоте и сигнал имеет постоянный уровень в пределах интервала измерения, то в спектре появляется одна дополнительная линия на данной частоте и в дополнительном группировании нет необходимости. Но для того, чтобы передать информацию, сигнал модулируют. Влияние модуляции приводит к появлению спектральных линий, центрированных относительно частот сигнализации. Группирование интергармоник в соответствии с требованиями приложения А приводит к снижению ошибок, как и при группировании составляющих, показанных на рисунке С.3.
Во многих случаях используют частоты сигнализации, не кратные частоте . Пример непрерывного передаваемого сигнала 23 В на частоте 178 Гц, наложенного на третью и пятую гармоники, имеющие среднеквадратические значения 11,5 В, представлен на рисунке С.4. Дискретное преобразование Фурье, не обеспечивающее определение спектральной линии на частоте 178 Гц (явление "потери" сигнала), распределяет энергию сигнала на частоте 178 Гц близлежащим спектральным линиям. В данном случае интергармоническая группа порядка 3,5 (см. приложение А) содержит большую часть распределенной энергии. Значение группы равно 22,51 В (ошибка - только 2,15%).
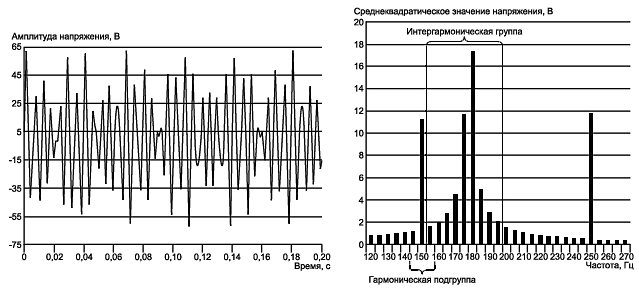
Рисунок С.4 - Передаваемый сигнал на частоте 178 Гц совместно с третьей и пятой гармониками
Примечания
1 Результатом "потери" сигнала на частоте, не кратной "базовой" частоте, является наложение дополнительных векторов на векторы первоначальных гармоник (см. рисунок С.7). Углы фазового сдвига между дополнительным и первоначальным вектором одной и той же частоты увеличиваются (или уменьшаются) на постоянное значение при переходе от одного интервала измерения (измерительного окна) к другому. В зависимости от угла фазового сдвига результирующий вектор может изменяться от суммы до разности этих векторов. В настоящем примере первоначальный вектор равен 11,5 В и дополнительные векторы равны 1,2 В на частоте 150 Гц и 0,4 В - на частоте 250 Гц (см. рисунок С.4). Результирующие векторы изменяются от 10,3 до 12,7 В на частоте 150 Гц и от 11,1 до 11,9 В - на частоте 250 Гц. Среднеквадратическое значение результирующего вектора, определенное на многих последовательных интервалах измерения, представляет собой "общее" среднеквадратическое значение первоначального и дополнительных векторов. В настоящем примере это 11,56 В на частоте 150 Гц и 11,51 В - на частоте 250 Гц. Процедура сглаживания, применяемая после группирования, значительно уменьшает возможные отклонения и обеспечивает получение средних значений, близких к общему среднеквадратическому значению.
2 Если уровень сигналов, передаваемых в системе электроснабжения, меньше, чем в настоящем примере, влияние указанных выше эффектов соответственно уменьшается.
Пример 2 - В системах электроснабжения могут иметь место интергармонические составляющие тока и напряжения, не связанные с передачей сигналов, случайно возникающие на частотах между двумя соседними гармониками. Например, на рисунке С.5 показана интергармоника 9,8 В на частоте 287 Гц совместно с пятой гармоникой 13,2 В и шестой гармоникой 10 В. В приведенном спектре виден эффект "потери" сигнала. Интергармоническая группа порядка 5 (см. 3.4) имеет значение 9,534 В (ошибка - 2,7%).
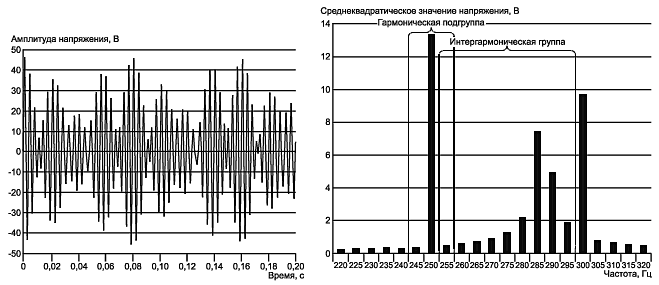
Рисунок С.5 - Интергармоника на частоте 287 Гц совместно с пятой и шестой гармониками
Пример 3 - Электродвигатель с изменяющимся моментом, например, приводящий в действие поршневой насос, инжектирует в систему электроснабжения пятую гармонику напряжения, среднее значение которой равно 10 В, модулированную синусоидальным сигналом частотой 5 Гц при коэффициенте модуляции 20% (см. рисунок С.6).
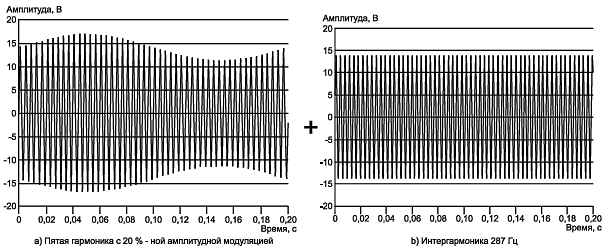
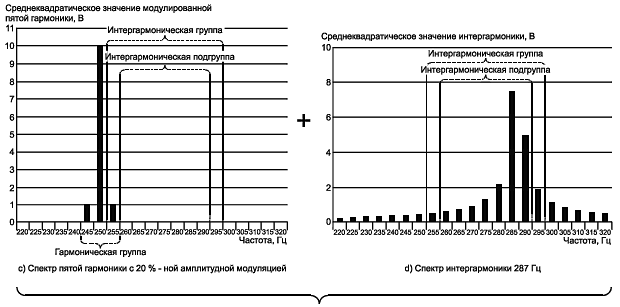
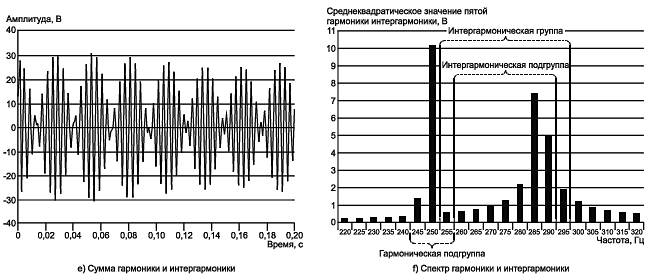
Рисунок С.6 - Модулированная пятая гармоника совместно с интергармоникой частотой 287 Гц
Общее среднеквадратическое значение функции времени, оцениваемое при интервале 0,2 с, равно 10,1 В. Спектр содержит линию "несущей" частоты 250 Гц и две боковых линии по 1 В на частотах 245 и 255 Гц (см. рисунок С.6с). Ошибка при учете одиночной спектральной линии 250 Гц будет равна 0,99%, при расчете гармонической подгруппы ошибка отсутствует.
В этой же системе электроснабжения может присутствовать сигнал 9,8 В на частоте 287 Гц (см. рисунок С.6в*). Из-за нецелого числа периодов данного сигнала в измерительном окне 200 мс (57,4 периода) возникает эффект "потери" сигнала. Среднеквадратическое значение интергармонической группы равно 9,538 В, ошибка - 2,7%.
________________
* Cоответствует оригиналу. - Примечание изготовителя базы данных.
Флюктуирующая гармоника и передаваемый сигнал складываются в системе электроснабжения (см. рисунок С.6е). Их общее среднеквадратическое значение равно 14,07 В. Возможны различные варианты группирования результирующих спектральных составляющих (рисунок С.6f). Так как спектр свидетельствует о наличии гармоники 250 Гц и сигнала вблизи частоты 285 Гц, возможно применение двух процедур группирования (каждая спектральная линия должна учитываться только один раз). При этом определяются:
- интергармоническая группа значением 9,36 В (ошибка 4,5% относительно 9,8 В) и единственная гармоническая линия значением 10,16 В (ошибка 1,6% относительно 10 В), что приводит к общему среднеквадратическому значению 13,81 В (ошибка 1,8% относительно 14,07 В);
- интергармоническая подгруппа значением 9,34 В (ошибка 4,7% относительно 9,8 В) и гармоническая подгруппа значением 10,23 В (ошибка 1,29% относительно 10 В), что дает общее среднеквадратическое значение 13,85 В (ошибка 1,5% относительно 14,07 В).
Вторая процедура группирования в большей степени соответствует "физике" процесса. Выбор процедуры группирования возможен после наблюдения спектра при нескольких последовательных интервалах измерения.
Боковые спектральные линии около пятой гармоники в наибольшей степени подвергаются влиянию эффекта "потери" сигнала. Для флюктуирующей пятой гармоники векторы составляющих 245 и 255 Гц равны по значению, но противоположно направлены. При неизменном коэффициенте модуляции длины векторов остаются постоянными, но их углы изменяются при переходе от одного интервала измерения к другому, так как частота модуляции не кратна "базовой" частоте. Векторы, связанные с интергармоникой 287 Гц, также остаются приближенно постоянными, но их углы изменяются от одного интервала измерения к другому. Две спектральных составляющих с частотами на 5 Гц выше и ниже частоты пятой гармоники представлены на рисунке В.7. Характеристики векторов, представленных на рисунке В.7, соответствуют интервалу измерения в соответствии с рисунком В.6. Длина вектора на частоте 245 Гц увеличена, а на частоте 255 Гц уменьшена вследствие воздействия векторов модуляции. В следующем интервале измерения углы векторов, связанных с интергармоникой 287 Гц, будут другими и, следовательно, величина объединенного вектора будет изменяться.
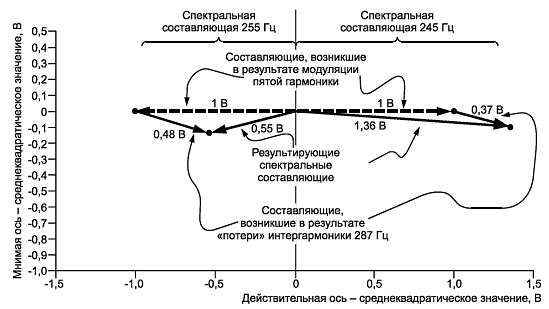
Рисунок С.7 - Векторы спектральных составляющих на частотах 245 и 255 Гц
|
