1.6.3.1. Выбор измерительных средств для контроля размеров

На рис. 3.3 показаны кривые распределения размеров деталей (y_тех) и погрешностей измерения (y_мет) с центрами, совпадающими с границами допуска. В результате наложения кривых y_мет и y_тех происходит искажение кривой распределения y(σ_тех, σ_мет), появляются области вероятностей m и n, обусловливающие выход размера за границу допуска на величину с. Таким образом, чем точнее технологический процесс (меньше отношение IT/Δ_мет), тем меньше неправильно принятых деталей по сравнению с неправильно забракованными.

Решающим фактором является допускаемая погрешность измерительного средства, что вытекает из стандартизованного определения действительного размера как и размера, получаемого в результате измерения с допустимой погрешностью.

Допускаемые погрешности измерения δ_изм при приемочном контроле на линейные размеры до 500 мм устанавливаются ГОСТ 8.051-81, которые составляют 35-20% от допуска на изготовление детали IT. По этому стандарту предусмотрены наибольшие допускаемые погрешности измерения, включающие погрешности от средств измерений, установочных мер, температурных деформаций, измерительного усилия, базирования детали. Допускаемая погрешность измерения δ_изм состоит из случайной и неучтенной систематической составляющих погрешности. При этом случайная* составляющая погрешности принимается равной 2σ и не должна превышать 0,6 от погрешности измерения δ_изм.

В ГОСТ 8.051-81 погрешность задана для однократного наблюдения. Случайная составляющая погрешности может быть значительно уменьшена за счет многократных наблюдений, при которых она уменьшается в √n раз, где n — число наблюдений. При этом за действительный размер принимается среднеарифметическое из серии проведенных наблюдений.

При арбитражной перепроверке деталей погрешность измерения не должна превышать 30% предела погрешности, допускаемой при приемке.

Значения допустимой погрешности измерения δ_изм на угловые размеры установлены по ГОСТ 8.050-73.

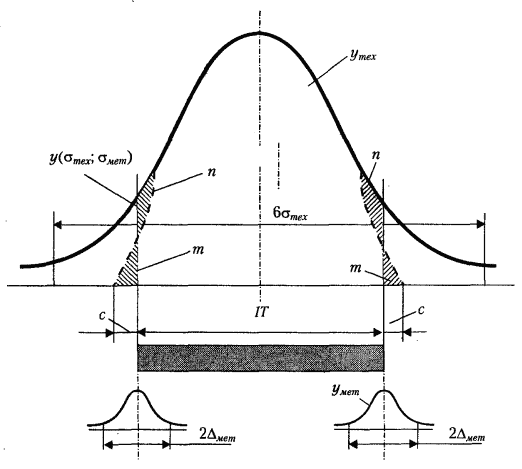
Рис. 3.3. Кривые распределения контролируемых параметров, построенные с учетом погрешностей измерения

Разрешается увеличение допустимой погрешности измерения, указанной в ГОСТ 8.051-81 и ГОСТ 8.050-73, при уменьшении допуска размера, учитывающего это увеличение, а также в случае разделения изделий на размерные группы для селективной сборки.

Установленные стандартом погрешности измерения являются наибольшими, которые можно допустить при измерении: они включают в себя случайные и неучтенные систематические погрешности измерении, все составляющие, зависящие от измерительных средств, установочных мер, температурных деформаций, базирования и т. д.

Случайная погрешность измерения не должна превышать 0,6 от допустимой погрешности измерения и принимается равной 2σ, где σ — значение среднего квадратического отклонения погрешности измерения.

• m — часть измеренных деталей, имеющих размеры, выходящие за предельные размеры, принята в числе годных (неправильно принятые);
• n — часть деталей, имеющих размеры, не превышающие предельных размеров, забракованы (неправильно забракованные);
• c — вероятностная предельная величина выхода размера за предельные размеры у неправильно принятых деталей.

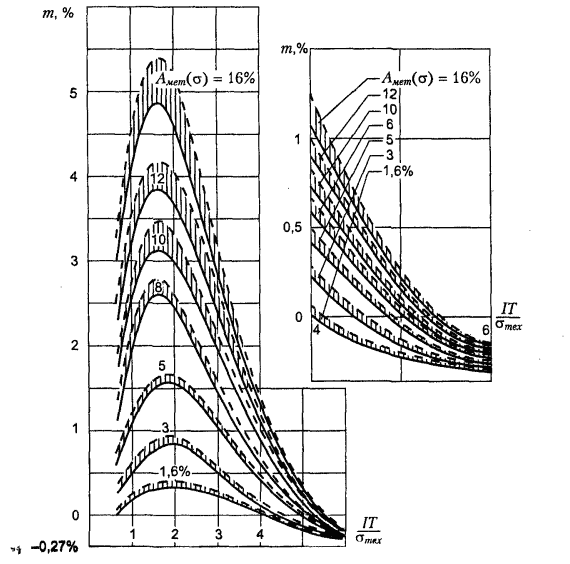
Рис. 3.4. График для определения параметра m

Значения параметров m, n, c при распределении контролируемых размеров по нормальному закону приведены на рис. 3.4-3.6.

Сплошные линии соответствуют распределению погрешности измерения по нормальному закону, а пунктирные — по закону равной вероятности.

При неизвестном законе распределения погрешности измерения для параметров m, n, c рекомендуется принимать средние их значения, определенных по сплошной и пунктирной линиям.

Параметры m и c на графиках определены с доверительной вероятностью 0,9973.

Для определения m с другой доверительной вероятностью необходимо сместить начало координат по оси ординат.

Кривые графиков (сплошные и пунктирные) соответствуют определенному значению относительной погрешности измерения, равной

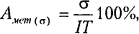
где	σ — среднее квадратическое отклонение погрешности измерения; IT — допуск контролируемого размера.

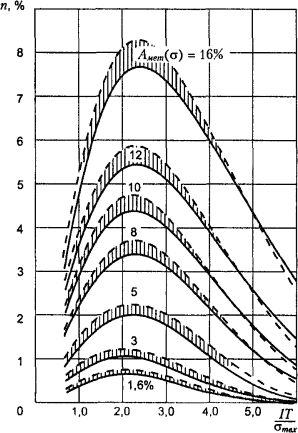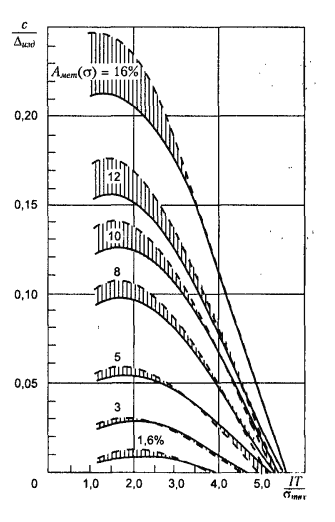
Рис. 3.5. График для определения параметров n	Рис. 3.6. График для определения параметров c

При определении параметров m, n, с  рекомендуется принимать A_мет(σ) = 16% для квалитетов 2-7, A_мет(σ) = 12% — для квалитетов 8 и 9, A_мет(σ) = 10% — для квалитетов 10 и грубее.

Параметры m, n, c приведены на графиках в зависимости от значения IT/σ_тех, где σ_тех — среднее квадратическое отклонение погрешности изготовления. Параметры m, n, c даны при симметричном расположении поля допуска относительно центра группирования контролируемых деталей. Для определения m, n, c при совместном влиянии систематической и случайной погрешностей изготовления пользуются теми же графиками, но вместо значения IT/σ_тех принимается для одной границы (IT + 2α_T)/σ_тех, a для другой — (IT — 2α_T)/α_тех, где α_T — систематическая погрешность изготовления.

При определении параметров m и n для каждой границы берется половина получаемых значений.

Возможные предельные значения параметров m, n, c/IT, соответствующие экстремальным значениям кривых (на рис. 3.4-3.6), приведены в табл. 3.5,

Таблица 3.5

Aтех(σ)	m	n	c/IT	Aмет(σ)	m	n	c/IT
1,60	0,37-0,39	0,70-0,75	0,01	10,0	3,10-3,50	4,50-,4,75	0,14
3,0	0,87-0,90	1,20-1,30	0,03	12,0	3,75-4,11	5,40-5,80	0,17
5,0	1,60-1,70	2,00-2,25	0,06	16,0	5,00-5,40	7,80-8,25	0,25
8,0	2,60-2,80	3,40-3,70	0,10

Первые значения m и n соответствуют распределению погрешностей измерения по нормальному закону, вторые — по закону равной вероятности.

Предельные значения параметров m, n c/IT учитывают влияние только случайной составляющей погрешности измерения.

ГОСТ 8.051-81 предусматривает два способа установления приемочных границ.

Первый способ. Приемочные границы устанавливают совпадающими с предельными размерами (рис. 3.7, а).

Пример. При проектировании вала диаметром 100 мм оценено, что отклонения его размеров для условий эксплуатации должны соответствовать h6(100-_0,022)- В соответствии с ГОСТ 8.051-81 устанавливают, что для размера вала 100 мм и допуска IТ = 0,022 мм допускаемая погрешность измерения σ_изм = 0,006 мм.

В соответствии с табл. 3.5 устанавливают, что для A_тех(σ) = 16% и неизвестной точности технологического процесса m = 5,0 и c = 0,25 IT, то есть среди годных деталей может оказаться до 5,0% неправильно принятых деталей с предельными отклонениями +0,0055 и -0,0275 мм.

Если полученные данные не повлияют на эксплуатационные показатели вала, то на чертежах указывают первоначально выбранный киалитет. В противном случае назначают более точный квалитет или другое иоле допуска в этом квалитете.

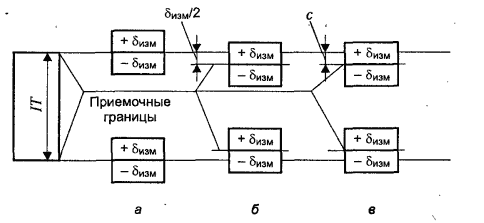
Второй способ. Приемочные границы смещают внутрь относительно предельных размеров.

При введении производственного допуска могут быть два варианта в зависимости от того, известна или неизвестна точность технологического процесса.

Вариант 1. При назначении предельных размеров точность технологического процесса неизвестна. В соответствии с ГОСТ 8.051-81 предельные размеры изменяются на половину допускаемой погрешности измерения (рис. 3.7, б). Для примера, рассмотренного выше, .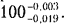

Вариант 2. При назначении предельных размеров точность технологического процесса известна. В этом случае предельные размеры уменьшают на значение параметра с (рис. 3.7, в).

Предположим, что для рассмотренного выше примера IТ/σ_тех = 4 (при изготовлении имеется 4,5% брака по обеим границам): A_мет (σ)= 16%, c/IT — 0,1; с = 0,0022 мм.

С учетом данных диаметр вала принимают 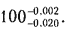.