Систематические и случайные погрешности
Систематической погрешностью называется погрешность, остающаяся постоянной или закономерно изменяющейся во времени при повторных измерениях одной и той же величины.
Примером систематической погрешности, закономерно изменяющейся во времени, может служить смещение настройки прибора во времени.
Случайной погрешностью измерения называется погрешность, которая при мно-гократном измерении одного и того же значения не остается постоянной. Например, при измерении валика одним и тем же прибором в одном и том же сечении получаются различные значения измеренной величины.
Систематические и случайные погрешности чаще всего появляются одновременно.
Для выявления систематической погрешности производят многократные измерения образцовой меры и по полученным результатам определяют среднее значение размера. Отклонение среднего значения от размера образцовой меры характеризует систематическую погрешность, которую называют «средней арифметической погрешностью», или «средним арифметическим отклонением».
Систематическая погрешность всегда имеет знак отклонения, то есть «+» или «-». Систематическая погрешность может быть исключена введением поправки.
При подготовке к точным измерениям необходимо убедиться в отсутствии постоянной систематической погрешности в данном ряду измерений. Для этого существуют специальные методы.
Прогрессивные и периодические систематические погрешности в противоположность постоянным можно обнаружить при многократных измерениях.
Обработка данных и оценка параметров случайных погрешностей производится методами математической статистики, изложенными в [42, 50].
При расчете предельной погрешности измерения определяют числовое значение погрешности измерения от всех составляющих и производят суммирование:
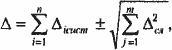
где знаки «+» или «-» ставятся из условия, чтобы систематические и случайные погрешности суммировались по модулю.
Если в случайной погрешности известно среднее квадратическое отклонение, то

где К — показатель, указывающий доверительные границы для предельной случайной погрешности измерения (при К = 1 р = 0,65; при К = 2 р = 0,945; при К = 3 р = 0,9973).
Если результаты измерений зависят от большого числа разнообразных факторов, то
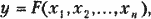
где Xi — переменные функциональные параметры.
Каждый параметр может иметь отклонение Δxi (погрешность) от предписанного значения xi. Поскольку погрешность Δxi мала по сравнению с величиной xi суммарная погрешность Δxy функции y можно вычислять по формуле:

где dy/dxi — передаточное отношение (коэффициент влияния) параметра xi.
Формула (3.1) справедлива лишь для систематических погрешностей Δxi.
Для случайных погрешностей (когда отдельные составляющие не всегда принимают предельные значения) используются теоремы теории вероятностей о дисперсии, то есть

Суммарная погрешность при наличии только случайных составляющих δxi погрешностей
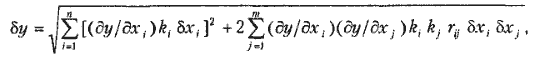
| где | m — число попарно корреляционно связанных параметров;
ki и kj коэффициенты относительного рассеяния, характеризующие степень отличия закона распределения погрешности данного параметра от нормального;
rij — коэффициент корреляции, существующий при наличии корреляционной связи между параметрами xi и xj
|
При наличии и систематических и случайных составляющих погрешностей вычисляют доверительные границы суммарной погрешности:
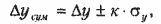
где k — масштабный коэффициент интервала распределения, зависящий от закона распределения и принятой доверительной вероятности.
Так, при доверительной вероятности Р = 0,95 для закона нормального распределения k= 2, а для закона Максвелла k = 3,6.
Пример. В результате измерений и последующего вычисления по формуле (3.1) получена суммарная систематическая погрешность результата измерения Δ= -0,7 мкм, среднее квадратическое этого результата измерения, вычисленное по формуле (3.2) σу = 0,4 мкм. Предел допускаемой погрешности δизм= +1 мкм. Тогда верхняя и нижняя доверительные границы погрешности при доверительной вероятности Р = 0,95.
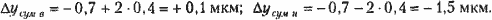
Так как Δyсум н>δизм, выбранный метод и средство измерения не удовлетворяют требованиям точности. Следовательно, необходимо скомпенсировать систематическую составляющую погрешности, например, путем изготовления образца для настройки измерительного средства. Размер образца должен быть больше его начального размера на 0,7 мкм; тогда будет справедливо неравенство 0,8 < 1 мкм и проведенные измерения будут удовлетворять требованиям по точности.
|
